Introduction

In today’s world, Travellers grapple with packing efficiently for various trips. This project addresses this challenge by developing an optimisation model to create optimal packing plans. The model leverages Operational Research techniques and considers factors like luggage weight restrictions, trip details, and item importance. By prioritising essential items and maximizing space utilisation, this model can generate packing plans that reduce stress, minimise the risk of exceeding weight limits, and ensure travellers bring everything they need for a smooth journey.

Project Identification and Description

In the present world, people travel for many reasons, such as education, work, or tourism. However, efficient packing is a practical challenge for every traveler. Whether going on a long weekend or a short business trip, optimising luggage capacity is very important to ensure all essential items are included in the bag while keeping the weight restrictions in check. These days there are many means of transport available,, and each means of transport differs in maximum luggage weight allowed. There are many companies involved in the transportation sector with different weight restrictions. Altogether, luggage capacity optimisation is a crucial part of a good travel experience. Efficient packing is not merely about fitting everything into a suitcase; it’s a strategic approach to organizing belongings to enhance convenience, mobility, and overall travel experience. By maximizing luggage space and adhering to weight restrictions, travelers can enjoy several benefits, including hassle-free transit, reduced stress, and cost savings.

This project aims to develop an optimisation model to reduce this manual and redundant task of adequate packing. It involves identifying essential and optional travel items, considering their weight and priority ratings based on trip characteristics (e.g., weather, trip duration, purpose). The goal is to create a packing plan that maximizes space utilisation while prioritising essential items.

Literature Review

Luggage packing is a universal travel woe. We all strive to maximise what we bring while staying within weight and space restrictions. Operational research (OR), the science of applying analytical methods to complex problems, offers a promising approach to optimising this common challenge. This review explores applying OR, precisely the Knapsack Problem (KP), to luggage packing. We examine the KP01 variant and its suitability for this task. The review then delves into the Dual Simplex Algorithm, a powerful tool for solving KP01 efficiently. Finally, we discuss the practical implementation of optimisation models and suggest avenues for future research.

The KP is a fundamental problem in OR, and it has a rich history dating back to the 19th century (Mathews, 1896). It was initially conceived to optimise essential item selection for soldiers (Millett, 1945). In its most basic form, KP involves selecting a subset of items from a collection, each with an associated weight and value, to maximise the total value while adhering to a weight constraint (Martello & Toth, 1987). This directly translates to the luggage packing scenario: maximising the number of valuable items (clothes, toiletries) packed within the weight limit of the suitcase.

KP comes in various forms, and for our purpose, the KP01 variant is particularly relevant (Lv et al., 2016). KP01 deals with selecting one or zero units of each item, perfectly aligning with the binary decision of packing an item or leaving it behind. While proven to be NP-hard (Rong & Figueira, 2012), signifying computational challenges for large datasets, KP01 offers practical solutions for real-world problems like resource allocation and project selection (Martello, Pisinger, & Toth, 2000).

Subject to:

Figure 1: Knapsack 0-1 mathematical formula (Martello and Toth,1987).

In Figure 1, the objective function is to maximise the profit by selecting a subset of items where Pj is the profit associated with item j, and xj is 1 if item j is packed; otherwise, it is 0. The objective function is subject to wj; the weight of item j, which is packed, is less than or equal to the maximum capacity c (Martello and Toth,1987).

Several algorithms can solve KP problems, and the Dual Simplex Algorithm stands out for its efficiency in solving mixed-integer linear programming problems like KP01 (Banciu, 2011). This algorithm iteratively refines a solution until it satisfies primal (original problem) and dual feasibility (related mathematical construct). (Banciu, 2011) details the steps involved in the Dual Simplex Algorithm given as follows:

• Step 0: (Initialization) Start with identifying dual feasible basis B for reduced cost vector c̅ = c−uTA is not negative.

• Step 1: (Pricing) If ~xB = B−1b is greater than or equal to 0, the current solution is optimal. Otherwise, select a pivot row i for the value of xi < 0. If there are multiple options, select the option with minimum value. The variable xi will leave the basis.

• Step 2: (Ratio test) If all constraint coefficients aij alongside the ith row are nonnegative (aij ≥ 0, ∀j), it means The dual problem is unbounded, and the primal problem is infeasible. Otherwise, performing the following minimum ratio test will give the pivot column j:

• The corresponding value of variable xj will be the basis.

• Step 3: (Basis change) Pivot on element aij and go to step 1. They illustrated the dual simplex method by contrasting it with the primal simplex. They used the traditional simplex tableau exposition, presented in the following fashion:

Note that in other treatments of linear programming, the reduced costs are defined the other way around, that is,c_N-c_BB^{-1}N. Under this interpretation, the arguments presented below still hold, but the signs are reversed. For example, the algorithm would terminate when all reduced costs are non-negative (in a minimisation example), rather than non-positive, as we assume.

Fortunately, optimisation models derived from OR principles can be implemented using readily available software tools. Microsoft Excel Solver, for instance, integrates a graphical user interface with algebraic modelling languages and solvers for various optimisation problems (Banciu, 2011). This seamless integration allows users to develop and solve optimisation models for luggage packing within a familiar spreadsheet environment.

While this review highlights the potential of OR for luggage packing, further research can explore advanced algorithms specifically tailored to this scenario. Luggage packing considerations extend beyond weight; factors like item volume also play a crucial role. Future research could investigate algorithms that handle weight and volume constraints, providing a more comprehensive packing solution.

Furthermore, empirical studies validating the effectiveness of optimisation models in real-world packing scenarios are crucial. Integrating technologies like artificial intelligence could enhance model accuracy and efficiency by learning from user preferences and packing habits. Finally, research into the environmental implications of optimised packing solutions is an exciting avenue. Minimising the weight and volume of packed luggage can reduce the travel industry’s carbon footprint, promoting sustainable luggage transportation.

In conclusion, this review demonstrates the applicability of OR, particularly the KP and Dual Simplex Algorithm, to optimise luggage packing. Researchers can develop innovative and practical solutions that empower travellers to pack efficiently and sustainably by exploring advanced algorithms, conducting real-world studies, and integrating new technologies.

Problem Modelling

The proposed model utilises mathematical optimisation techniques to determine the optimal packing plan. Formulating the problem as a binary integer programming model based on the Knapsack problem seeks to maximise the objective function subject to weight constraints and mandatory item inclusion requirements. The objective is to prioritise the essential items, Balance weight constraints, Consider the trip specifics and maximise the luggage space utilisation. The model deals with several parameters as given below:

• User Inputs Parameters:
  • B = Maximum Allowed Weight of the Bag.
  • N = Total Number of items considered for packing.
  • Wi = Weight of item i (in Kg).
  • Trip_Weather = The user defines trip destination weather (hot or cold).
  • Trip_Type = Type of trip (international or domestic) defined by the user.
  • Trip_Length = The length of the trip (long or short) is defined by the user.
• Calculated Parameters:
  • Ari = Average Rating of item i.

Here, B is the maximum weight of the luggage allowed in kilograms based on the user requirements. Three trip specifics are considered in the model: Trip_Weather, Trip_type, and Trip_Length. Based on these trip specifics, a rating is given to each item N on the list. Wi is the weight of item i and the average rating Ari of each item i is calculated based on the user-selected trip specifics. In the actual mode, the Average rating Ari is used for optimisation, not trip-specific ratings. An objective function is created on the basis of the Knapsack problem also known as KP01. As shown in Figure 2, This objective function maximises the Average rating by selecting only the important items from the list of items. Here, xi defines the integer part of the equation. It is 1 for all the selected items and 0 for all others.

This Objective function is subject to a few constraints that help this model optimise the solution based on user requirements. In Figure 3, the first constraint is defined which restricts the model to select all the items optimally while keeping the sum of the weight of all the selected items less than or exactly to the maximum weight defined by the user. The last and most important constraint is to pack all the mandatory items. In Figure 4, it is shown that a subset MandatoryItems consisting of the items made mandatory by the user is always selected.

\(\sum_{i=1}^{N} w_i \cdot x_i \leq B\)

Problem-Solving

Continuation with the Mathematical modelling. This whole modelling is made in Microsoft Excel with a solver add-in. To practically implement this model spreadsheet modeling technique is used. First is a list of items that can be packed is considered. This list is kept short, but practically, it can go up to millions of items. To keep this possibility as a feasible construct of the model. This part is kept user-defined. For this model, a total of 52 most common items are considered. There, a rating system is introduced for each item; each item can be rated from 0 to 10, where 10 is the highest. For effective packing for travel, trip specifications are the primary constraints that drive the packing. In this model, three such trip specifications are considered. Firstly, it consists of the Weather of the destination, whether it is hot or cold; ratings of each item are done on this basis. For example, a hat is rated more for a hot climate and less for a cold climate. Similarly as shown in Figure 5, each item is rated for the type of travel, domestic or international travel, and the length of the travel, whether short or long. All the ratings are user-defined to address the user’s preferences accurately, making this model general purpose for any user. We also consider each item’s weight; one of our final aims is to optimise the weight limit of the bag.

To make this model user-friendly, the user can input the exact weight in kgs and select trip specifics from the drop-down menu as shown in Figure 6. Based on the item’s trip specifics and corresponding ratings, a new table is formed as shown in Figure 7, with the average rating of each item. A new column is also introduced where the user can define if a particular item is mandatory to take by selecting priority as yes from the drop-down. The average rating of each item is calculated as follows:

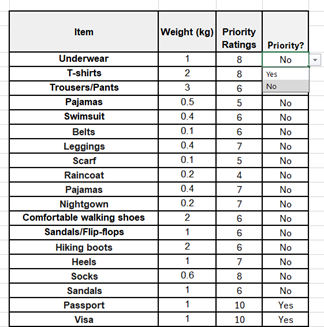
Using the average rating function and all the other parameters, an optimisation model is made using an Excel solver add-in. Figure 8 shows the solver parameters according to mathematical formulations.

Solution Analysis

The solution generated by the optimisation model reflects a packing plan that balances item rating, weight constraints, and trip specifics. By prioritising essential items and considering trip characteristics, the solution enhances packing efficiency and reduces the risk of issues such as exceeding baggage weight limits or forgetting crucial items. The analysis includes evaluating the effectiveness of the packing plan in various travel scenarios. Figure 9 shows the output of the model. Some items are selected, and some are not, whereas Figure 10 shows that the model can successfully include all the mandatory items. There are some extra zeros below mandatory items as this list can grow or shrink based on the user selection of mandatory items to cover this by solver parameters are modifed.

Some custom matrices are included in the spreadsheet to help understand the model’s performance. Figure 11 shows that the model was used with a maximum luggage weight allowed of 23 Kg. There were 52 Items in the list, and its overall weight was 44.2 Kg. However, the Model successfully optimised the Luggage packing by selecting 42 Items while Keeping the weight of all the items under 23 Kg. Another Custom metric is the overall average rating of the final average rating table. The overall average rating of 52 items was 6, and the optimisation model successfully increased it while 80% of the items were included.

Conclusion

This project explored an optimisation model for luggage packing, demonstrating the value of Operational Research (OR) and Business Optimization (BO) in a real-world context. Based on the Knapsack Problem, the model showcases how OR techniques can create efficient solutions for business problems like luggage restrictions. By optimising packing, travellers potentially reduce baggage fees, impacting travel decisions and airline revenue. The model’s effectiveness highlights its usefulness for travellers. User inputs and item characteristics are analysed to generate space-maximized packing plans prioritising essentials. This reduces packing stress, minimises weight limit issues, and ensures travellers bring everything needed. This translates to BO for travel service providers by potentially reducing customer service issues and baggage handling costs.

Personally, I believe this project provided valuable insights into applying OR and BO principles. It emphasised the power of mathematical modelling for optimising decision-making, not just for travellers but also for businesses in the travel industry. The user-centric design approach reinforces the importance of practicality in BO solutions. These learnings extend beyond luggage packing and can be applied to other resource-constrained scenarios within the travel sector.  

References

• Banciu, M., 2011. Dual simplex. In Wiley Encyclopedia of Operations Research and Management Science. Wiley.

• Duckworth, W.E., 2012. A guide to operational research. Springer Science & Business Media.

• Fourer, R., Gay, D.M. and Kernighan, B.W., 1990. A modeling language for mathematical programming. Management Science, 36(5), pp.519-554.

• Lv, J., Wang, X., Huang, M., Cheng, H. and Li, F., 2016. Solving 0-1 knapsack problem by greedy degree and expectation efficiency. Applied Soft Computing, 41, pp.94-103.

• Martello, S., Pisinger, D. and Toth, P., 2000. New trends in exact algorithms for the 0–1 knapsack problem. European Journal of Operational Research, 123(2), pp.325-332.

• Martello, S. and Toth, P., 1987. Algorithms for knapsack problems. North-Holland Mathematics Studies, 132, pp.213-257.

• Mathews, G.B., 1896. On the partition of numbers. Proceedings of the London Mathematical Society, 1(1), pp.486-490.

• Millett, J.D., 1945. Logistics and Modern War. Military Affairs: Journal of the American Military Institute, pp.193-207.

• Rong, A. and Figueira, J.R., 2012. Computational performance of basic state reduction based dynamic programming algorithms for bi-objective 0–1 knapsack problems. Computers & Mathematics with Applications, 63(10), pp.1462-1480.

• Rosenthal, R.E., 2007. A gams tutorial. GAMS-A User’s Guide, 5(26), p.649.

• Saleh, S.A. and Latif, T.I., 2009. Solving Linear Programming Problems By Using Excel’s Solver. Tikrit J. Pure Sci, 14, pp.87-98.

Disclaimer

This report was originally submitted as part of the coursework requirements for the Master of Science in Data Science and Analytics at the University of Westminster. The content reflects the author's academic research and findings at the time of submission.

While efforts have been made to ensure accuracy, the report may not be free from errors or may not reflect the most current developments in the field. The views and conclusions expressed are those of the author and do not necessarily represent those of the University of Westminster or any affiliated institution.

This document is provided for informational and educational purposes only. It should not be used as a substitute for professional advice or as an official representation of industry standards. The author and the University of Westminster disclaim any liability for any direct or indirect consequences resulting from the use of this material.

For any inquiries or permissions regarding the reproduction of this work, please contact the author.